aaspot.blogg.se - Parallel resistance formula

#Parallel resistance formula series#

Draw a clear circuit diagram, labeling all resistors and voltage sources.

#Parallel resistance formula series#

Problem-Solving Strategies for Series and Parallel Resistors Why do lights dim when a large appliance is switched on? The answer is that the large current the appliance motor draws causes a significant IR drop in the wires and reduces the voltage across the light. For example, if current flows through a person holding a screwdriver and into the Earth, then \boldsymbol), which then dims noticeably. When are resistors in series? Resistors are in series whenever the flow of charge, called the current, must flow through devices sequentially. The total resistance of a combination of resistors depends on both their individual values and how they are connected. The simplest combinations of resistors are the series and parallel connections illustrated in Figure 1. Using this resistor in parallel formula, it is very easy to calculate the total equivalent resistance of resistors in parallel. A measure of this limit on charge flow is called resistance. The standard formula for calculating the total resistance for a number of resistors in parallel is given below. Most circuits have more than one component, called a resistor that limits the flow of charge in the circuit.

Calculate total resistance of a circuit that contains a mixture of resistors connected in series and in parallel.

Explain why total resistance of a parallel circuit is less than the smallest resistance of any of the resistors in that circuit.

Contrast the way total resistance is calculated for resistors in series and in parallel.

Calculate the voltage drop of a current across a resistor using Ohm’s law.

Draw a circuit with resistors in parallel and in series. In the case of a parallel configuration, each resistor has the same potential drop across it, and the currents through each resistor may be different, depending.

We don’t know how $i$ splits up into the three resistor currents.

We don’t yet know voltage $v$ appearing across the resistors and current source.

With just this little bit of knowledge, and Ohm’s Law, we can find the things we don’t know,

Voltage $v$ appears across all three resistors.

The currents in the three resistor have to add up to $i$.

Current $i$ is some given constant value. The above equation shows that if R1 is equal to R2, then Req is half of the value of one of the two resistors.

but we don’t yet know the voltage $v$ or how $i$ splits up into the three resistor currents. Current $i$ returns to the bottom terminal of the current source. We don’t get to use those very often, so this should be fun.Ĭurrent source $\text I_\text s$ is driving current $i$ toward $\text R1$, $\text R2$, and $\text R3$. Here is a circuit with resistors in parallel. This circuit has four separate nodes, so $\text R1$, $\text R2$, and $\text R3$ do not share the same voltage. Is there any easy function to calculate parallel and series of resistors when i tried its showing error Wrong number of input arguments for obsolete. The formula for three resistors connected in parallel is: 1 Rges 1 R1 + 1 R2 + 1 R3 1 R g e s 1 R 1 + 1 R 2 + 1 R 3.

There are extra components (orange boxes) breaking up the common nodes between resistors. The conductance is the reciprocal of the resistance. The resistors in the following image are not in parallel. Another good resource to help you understand parallel circuits is this article on Schematic equivalence.īecause the resistors are connected to the same nodes, the same voltage appears across each parallel resistor. Review the definitions of node and a distributed node in this article on Circuit terminology. The two horizontal lines represent the two nodes shared by all three resistors. In the following image, $\text R1$, $\text R2$, and $\text R3$ are in parallel. The formula for resistors in parallel is, 1/Rp (1/2) +(1/4)+(1/6) 1/Rp 11/12.

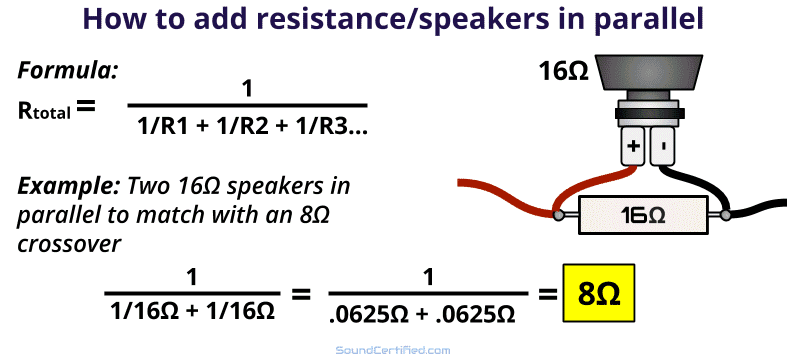
Special case - $2$ equal resistors in parallelĬomponents are in parallel when their two terminals connect to the same nodes.Special case - $2$ resistors in parallel.Current distributes between resistors in parallel.The current flowing in resistor R2 is given as: IR2 VS R2 12V 47k 0.255mA or 255A. Figuring out parallel resistors is a little trickier than series resistors. By using Ohm’s Law, we can calculate the current flowing through each parallel resistor shown in Example No2 above as being: The current flowing in resistor R1 is given as: IR1 VS R1 12V 22k 0.545mA or 545A. We reveal the properties of the parallel connection by looking at resistor circuits. Components are in parallel if they share two nodes, like this,